İntegralHacim Maddelerin uzayda kapladığı yere hacim denir. İki madde birlikte aynı hacmi işgal edemez. Örneğin bir bardağa su konulduğunda bardağın içindeki hava, kabı terkeder.
İntegral veya Tümlev, bir fonksiyon eğrisinin altında kalan alanıdır; başka bir deyişle, fonksiyonun türevinin tersi olan bir fonksiyon elde edilmesini sağlar.
Tanım
İntegral, verilen bir f(x) fonksiyonunu türev kabul eden F(x) fonksiyonunun bulunması olarak yapılabilir. F(x)fonksiyonuna f(x) fonksiyonunun integrali veya ilkeli denir. İntegral, Latince toplam kelimesinin ("summa") baş harfi s'nin biraz evrim geçirmiş hali olan ∫ işareti ile gösterilir. Bu işaret Leibniz tarafından tanımlanmıştır.
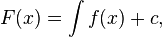
c bir sabiti gösterir ve integralin bir sabit farkı ile bulunabileceğine işaret eder.
Bir eksen takımında gösterilen f(x) göndermesinin altında kalan a < x < b aralığındaki alan, integral yardımıyla hesaplanabilir. Bu amaçla alan küçük dikdörtgenlere bölünerek, bunların alanı hesap edilip toplanır. Dikdörtgen sayısı arttıkça toplam eğri altındaki alan, alanın değerine yaklaşır ve integralin tam değeri bulunmuş olur. Bu toplama Riemann toplamı denir. İntegralin Riemann anlamındaki tanımı Riemann toplamındaki bölüntü sayısı olan n nin bir limit içerisinde sonsuza götürülmesiyle elde edilir.

Bu şekildeki integral belirli sınırlar arasında hesaplandığı için, belirli İntegral olarak isimlendirilir. Sınırlar göz önüne alınmadan hesaplanan integrale ise belirsiz integral denir. Bazı durumlarda f(x) göndermesinin integrali F(x)bulunamaz. Bu durumda belirli integral sayısal olarak hesaplanır.
Uzunluk, alan ve hacimlerin hesaplanmasında integral hesabın önemli yeri vardır. Birden fazla değişkene bağlı fonksiyonlarda integral kavramı genişletilebilir ve bu durumda katlı integraller ortaya çıkar.
Riemann'dan sonra soyut kümelerin de integrallenebilmesi amacıyla Lebesgue integrali geliştirilmiştir.
Köken
- Dilimize İngilizceden veya Fransızcadan geçmiş integral sözcüğü "bütüne ait olan" anlamına gelir ve İngilizceye Orta Fransızca intégral sözcüğünden; Orta Latince integralis (tüm yapmak, tümlemek) sözcüğünden; Latince integer(tüm, bütün, tam) sözcüğünden gelmiştir. Ayrıca integer sözcüğü tam sayı terimine karşılık olarak İngilizceye geçmiştir.
- Türkçede tümlev sözcüğü, Osmanlıca mütemmem ile tamamî sözcüklerinin ve İngilizcedeki integral sözcüğünün anlamını karşılamak için türetilmiştir. tümlev sözcüğü, "tümlenmiş şey" anlamına gelir. İsimden fiil yapan /-ev,-av/yapım ekiyle kullanımda olan tümle[mek] fiilinden; isimden fiil yapan /-le[mek]/ yapım ekiyle muhtemelen Öz Türkçe *tüm (bknz. tümen) kökünden türetilmiştir.
- Osmanlıcada mütemmem sözcüğü kullanılmış (Arapçadaki *tm (tam) kökünden gelir) ancak Arapçada şu anda "olgun, evrimleşmiş, bütünleşmiş" anlamındaki tekâmül sözcüğü kullanılmaktadır(kâmil, mükemmel, küme ile aynı kökten: *kml).
İntegral alma yöntemleri
Değişken değiştirme
Basit fonksiyonların integrallari
Rasyonel fonksiyonlar
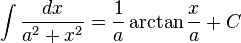
İrrasyonel fonksiyonlar

Logaritmik fonksiyonlar


Üslü fonksiyonlar
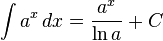
Trigonometrik fonksiyonlar

Hiperbolik fonksiyonlar

Ters hiperbolik fonksiyonlar
f(x)'in a dan b'ye kadar olan integrali, y=f(x) fonsiyonunun a ile b arasındaki alanıdır.
Katı maddelerin belli bir şekli ve hacmi vardır. Sıvı maddelerin belli bir hacimleri olmasına rağmen belirli bir şekilleri yoktur, konuldukları tabın şeklini alırlar. Gazların ise hem belirgin hacimleri hem de belirgin şekilleri yoktur. Konuldukları kapların hacmini ve şeklini alırlar.
Geometrik Biçimli Cisimlerin Hacimleri
Geometrik şekilli, dikdörtgenler prizması, küp, silindir, küre ve koni şeklindeki katı cisimlerin hacimleri, boyutları ölçülerek hesaplanır.
Dikdörtgenler prizmasının hacmi farklı üç kenarının çarpımına eşittir.

Hacim = En . boy . yükseklik
V = a . b. c dir.
Üç kenarı da eşit ve a kadar olan küpün hacmi
V = a3 dür.
Taban yarıçapı r, yüksekliği h olan silindirin hacmi, taban alanı ile yüksekliğinin çarpımına eşittir.
V = pr2 . h dir.
Yarıçapı r olan kürenin hacmi



Düzgün Olmayan Cisimlerin Hacimleri
Düzgün geometrik yapıda olmayan katı cisimlerin hacimleri, dereceli kaplardaki sıvılardan yararlanılarak bulunur.
Bu tür cisimler tamamen sıvı dolu olan bir kaba batırıldığında, sıvıda erimemek şartıyla hacmi kadar hacimde sıvı taşırır. Eğer cisim tamamen batmıyorsa, taşan sıvının hacmi batan kısmın hamine eşit olur.

Tamamen dolu olmayan dereceli kaptaki sıvıya bir cisim atılırsa, cismin hacmine eşit hacimde sıvıyı yer değiştirir.
Eğer katı bir cisim sıvı içine atıldığında çözünüyorsa, cismin gerçek hacmini bulamayız. Çünkü, cismin katı haldeki hacmi ile sıvı haldeki hacmi eşit olmadığı gibi, katı içinde hava boşlukları olabilir ve eridiğinde hava çıkar ve hacim azalır.
Dereceli kapta bulunan kuru kumun üzerine su döküldüğünde, karışımın hacmi, su ve kumun ayrı ayrı hacimlerinin toplamından daha küçük olur. Bunun nedeni, kum tanecikleri arasında hava boşluğu olması ve suyun bu boşlukları doldurmasıdır. Buna göre, kumun gerçek hacmi, karışımın hacminden suyun hacmi çıkarılarak bulunur.
Hacim Birimleri
Hacim V sembolü ile gösterilir. SI birim sisteminde hacim birimi m3 tür. Pratikte maddelerin hacmini ölçmek için m3 ün alt katları olan cm3 ve dm3 kullanılır. Bir cismin hacmi bulunurken, üç boyutu çarpıldığı için, hacim birimleri de uzunluk birimlerinin küpü olarak ifade edilir.
1 m3 =1000 dm3
1 dm3 =1000 cm3 = 1 Litre
1 cm3 =1000 mm3Hacim ölçüleri 1000 in katları olarak artar. 1 litrenin 1 dm3 e eşit olduğu bilinirse, litre birimi diğer birimlere kolaylıkla çevrilebilir. Hacim Ölçüleri:
1 Metrekup (m³) 1 m³
1Dekametre kup (Dm³).....= 1000 m³
1Hektometre kup (hm³).... =1.000.000 m³
1Kilometre kup (Km³) .......=1.000.000.000 m³
1Desimetre kup (dm³) ......=1/1.000 m³
1Santimetre kup (cm³)......= 1/1.000.000 m³
1Milimetre kup (mm³) .......=1/1.000.000.000 m³
Hacim Ölçüleri: (Sıvılar için):
1 Litre (l) 1 l
1Dekalitre (dal) =.....10 l
1Hektolitre (hl) =......100 l
1Kilolitre (kl) =.........1.000 l
1Desilitre (dl) =........1/10 l
1Santilitre (sl) =.......1/100 l
1Mililitre (ml) =........1/1.000 l
SORULAR VE ÇÖZÜMLERİ:


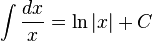

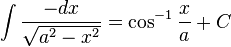
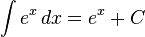



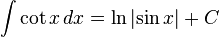








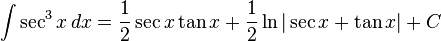
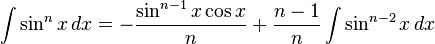












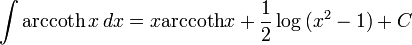

 fonksiyonu verilmiş olsun.
fonksiyonu verilmiş olsun.
 ile gösterilir. Buna göre,
ile gösterilir. Buna göre,














 verilsin.
verilsin.  olmak üzere,
olmak üzere,










 fonksiyonu
fonksiyonu  şeklinde belirtilebileceği gibi, g ve h iki fonksiyon olmak üzere
şeklinde belirtilebileceği gibi, g ve h iki fonksiyon olmak üzere


 olmak üzere,
olmak üzere, ifadesine
ifadesine ifadesine de y = f(x) in n.
ifadesine de y = f(x) in n.

